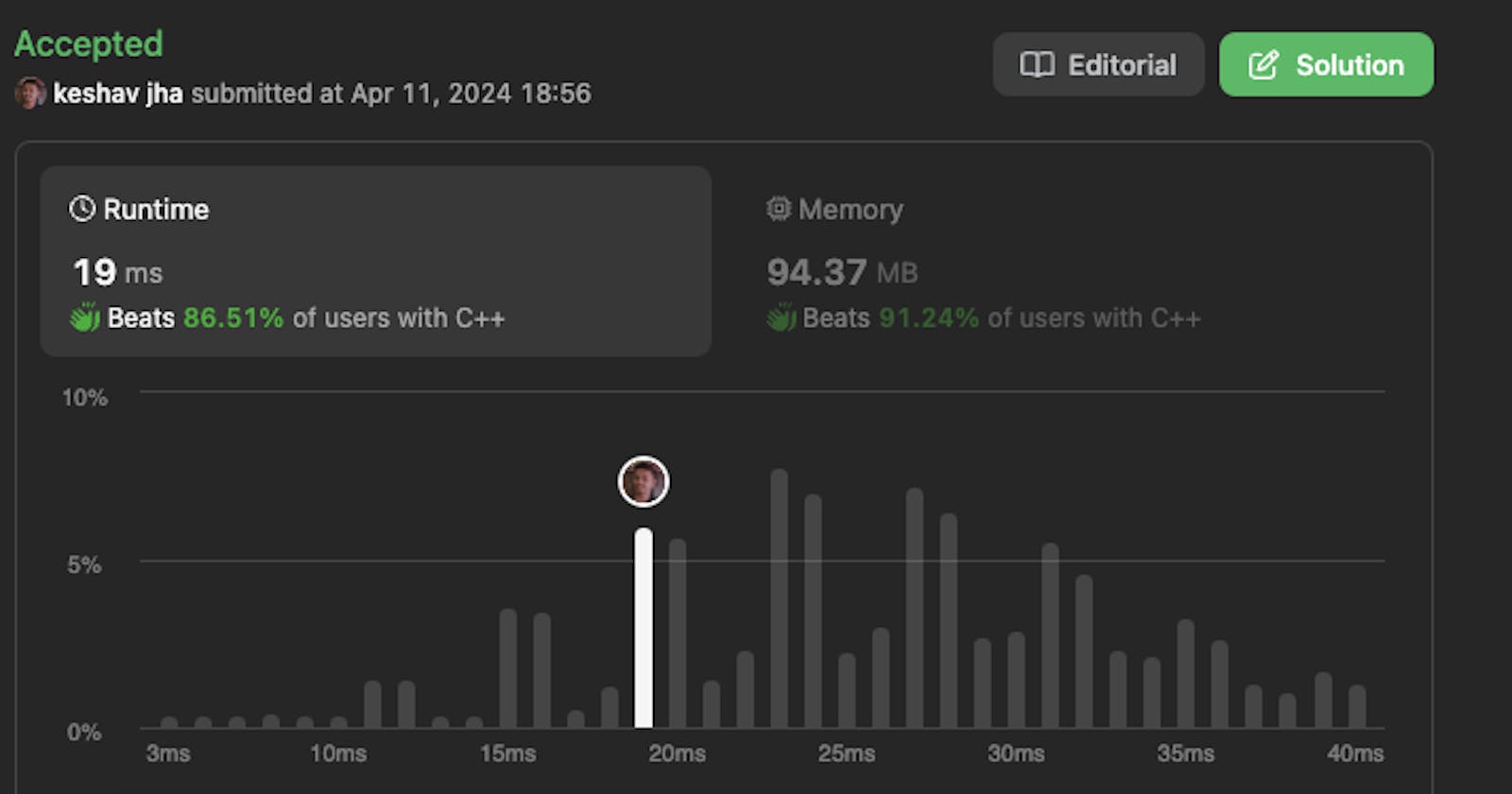
leetcode: Median of Two Sorted Arrays Problem in C++

Introduction:

Finding the median of two sorted arrays efficiently. In this blog post, we'll explore how to solve this problem in C++, achieving a runtime complexity of O(log(m+n)).

Problem Statement:

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be O(log (m+n)).

Example 1:

Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example 2:
Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Constraints:

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

Approach:

To solve this problem efficiently, we'll utilise the binary search algorithm. The key insight is to partition the arrays nums1 and nums2 into two parts such that the elements on the left side are smaller than or equal to the elements on the right side. This partition should be such that the length of the left partition is equal to or one element larger than the length of the right partition.

Algorithm:

Ensure nums1 is not larger than nums2. If it is, swap them.
Initialize low and high as 0 and the length of nums1, respectively.
Perform a binary search on nums1 to find the correct partition partN1.
Calculate the corresponding partition partN2 in nums2.
Determine the maximum elements (mxLN1 and mxLN2) on the left side and the minimum elements (minRN1 and minRN2) on the right side.
Check if the partitioning is correct, ensuring that mxLN1 <= minRN2 and mxLN2 <= minRN1.
If the partitioning is correct, calculate the median based on the lengths of nums1 and nums2.
Adjust low and high based on the comparison of mxLN1 and minRN2.
Repeat the binary search until the correct partition is found.

Code C++

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        unsigned int n = nums1.size(), m = nums2.size();

        if (n == 0 && m == 0)
            return double(0);

        if (n == 0) {
            if (m % 2 == 0) {
                return (nums2[m / 2 - 1] + nums2[m / 2]) / 2.0;
            } else {
                return nums2[m / 2];
            }
        }

        if (m == 0) {
            if (n % 2 == 0) {
                return (nums1[n / 2 - 1] + nums1[n / 2]) / 2.0;
            } else {
                return nums1[n / 2];
            }
        }

        if (n > m) {
            return findMedianSortedArrays(nums2, nums1);
        }

        int low = 0, high = n;

        while (low <= high) {
            int partN1 = (low + high) / 2;
            int partN2 = (n + m + 1) / 2 - partN1;

            int mxLN1 = (partN1 == 0) ? INT_MIN : nums1[partN1 - 1];
            int minRN1 = (partN1 == n) ? INT_MAX : nums1[partN1];

            int mxLN2 = (partN2 == 0) ? INT_MIN : nums2[partN2 - 1];
            int minRN2 = (partN2 == m) ? INT_MAX : nums2[partN2];

            if (mxLN1 <= minRN2 && mxLN2 <= minRN1) {
                if ((n + m) % 2 == 0) {
                    return (max(mxLN1, mxLN2) + min(minRN1, minRN2)) / 2.0;
                } else {
                    return max(mxLN1, mxLN2);
                }
            } else if (mxLN1 > minRN2) {
                high = partN1 - 1;
            } else {
                low = partN1 + 1;
            }
        }

        return 0.0;
    }
};

Code Explanation:

We handle edge cases where one of the arrays is empty or both arrays are empty.
We ensure that the length of nums1 is smaller or equal to the length of nums2.
We perform a binary search to find the correct partition in nums1.
We calculate the corresponding partition in nums2.
We check if the partitioning is correct and calculate the median accordingly.
We adjust the search space based on the comparison of elements.

Complexity Analysis:

Time Complexity: O(log(min(m, n))) - The binary search is performed on the smaller array.
Space Complexity: O(1) - Only a constant amount of extra space is used.

Conclusion:

We discussed how to efficiently solve the median of two sorted arrays problem in C++ using a binary search approach. By partitioning the arrays intelligently, we were able to achieve a runtime complexity of O(log(m+n)).